Trigonometry and Architecture, Statistics Problem Example

Introduction

Architecture and mathematics share a search for order and beauty in the world; mathematics finds order in nature and architecture finds beauty in construction. The disciplines are interdependent as architecture relies on mathematical developments to promote structural concepts and calculations. Through the use of mathematics, architecture creates structures which coexist harmoniously within any given environment. It is within this context that geometry became a guiding principle in the architectural field. Geometric construction dates back to 300 BC when the Greeks employed the number Phi to plan and construct structures; most specifically, the Parthenon. This was considered the foundation of the use of mathematics in architecture. A few centuries later, calculus became the architectural principle of choice in the construction of new buildings. This paper will examine the use of calculus in Gothic architecture.

Background

Gothic architecture originated in France in 1140. Paris in 1140, was not only the capital of France, it was also the ‘royal city,’ (Toman). Abbott Suger of St. Denis initiated the Gothic architectural style in response to France’s desire to emerge as a fashion-forward society. He combined Norman and Burgundian architecture and called it Gothic. Norman architecture was famed for its use of ribbed vaults and Burgundian architecture was famed for its pointed arches. His creation was immensely popular and nearly 80 cathedrals in the Gothic style were built between 1180 and 1270 in France.

The most defining characteristic of Gothic architecture is its use of the ogival or pointed arch. This particular style offered enhanced design flexibility to the architect because it allowed an abundance of light into the building, as a result of the vaulted windows and ceilings. Buildings of the Norman and Burgundian styles did not offer similar architectural opportunities because its arches were more semi-circular (Toman). Thirteenth-century Picard architect, Villard de Honnecourt, was the first to discuss pointed arches. He also coined the term ‘ogive’. Ogive refers to a curved and pointed surface which is used to form the streamlined nose of a projectile. It is formed through the creation of a surface of revolution with a curve. Today, this curve is called a Gothic arch (Branner). Compared to the Romanesque style before, Gothic architecture had pointed arches, instead of round arches; had flying buttresses, instead of wall mass; and had open tracery, instead of walls with niches. The Gothic style allowed its structures to absorb more light.  As a result, stained glass rose windows reflected light and color onto the interior walls of cathedrals, creating a colorful and spacious collage of light.

Construction of Gothic buildings depended on the availability of materials. Different European countries had varying materials in varying availabilities, which resulted in deviations of Gothic structures from region to region. For instance, France had an abundance of limestone, which was used for sculptural decorations within and on top of Gothic cathedrals. England had an abundance of timber, which was unseasoned, short, and crooked. This resulted in magnificent hammer-beam roofs of its gothic structures. Germany and the Netherlands had an abundance of bricks. In fact, the use of brick in Germany, the Netherlands, Scandinavia, and northern Poland, resulted in the Brick Gothics style. Italy incorporated its abundance of marble into its structures by covering the front of Gothic cathedrals with it.

Gothic Architecture

The most prominent feature of Gothic architecture is its use of arches. The Gothic arch has a relatively large rise-to-span ratio, with sides that consist of circles and centers that are at the level of the spring line. They are typically separated into three sub-groups: the equilateral arch, the lancet arch, and the drop arch (Huber). The spring line of the Gothic arch is a horizontal line, which intersects the beginning of the arch, or the springing. The spring line, therefore, encompasses the span of the arch. The span is the horizontal dimension, or the width of the arch from A to B. The rise is the height of the arch from O to C.

Figure 1: The Gothic Arch

Gothic opening as typically based on the equilateral arch form. This means that the radius of the arch is the width of the opening and the center of each opening corresponds with the point from which the opposite arch originates. In other words, the arch is higher in relation to its width. The radius equals the distance from A to B in Figure 1.

Calculation of the Gothic Arch

During 13^th century France, proponents of the Gothic arch argued that it should have a radius of one length-unit less than its span. This was called the quinto acuto, or fifth-point arch. The fifth-point arch has a radius-to-span ratio of four fifths. In other words, if the arch’s span in 5m then the radius of each arch is 4m. Also called a drop arch, it was labeled with positive integers (Toman). The fifth-point arch consists of two quarter circles, which are pressed together to support the weight of the arch above it. This was particularly important for stained glass windows and domes. So, the arch center is inside the span of the arch, and not directly underneath the tip of the arch.

If the horizontal distance from the center of the arch is 2 meters across to either side of the arch’s bottom edge, it would give an overall entrance of 2 meters across. This means that the center of each arch is 2m/5m from the opposite end. That would mean that the arch which starts on the left side and goes upward and right, is centered at the point 3m/5,0 and it has a radius of r=8m/5. This is achieved though the sum of m + 3m/5. This is achieved through the use of the following equation:

The distance from the center of the arch is given by the point:

(x, y) = (0,0) which is the origin.

So, the opposite arch will be centered at (-3m/5,0) with the same radius.

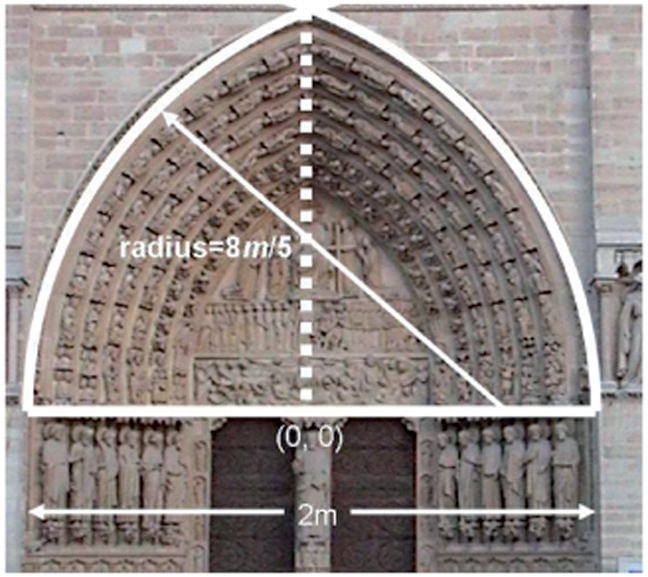
Figure 2: The Radius and the quinto acuto Arch

Conclusion

Gothic architecture is a prime example of a real-world integration technique. Mathematics and Gothic architecture are interrelated and the tracery of Gothic windows offers various examples of geometry and area through the use of calculus. All Gothic architecture provides trigonometry problems that can be solved through the use of simple equations. Mathematics, and specifically calculus, offered a viable solution to the problem of Gothic architecture; specifically the immense weight of the actual buildings. The solution to the weight problem was the use of arched openings. By incorporating an arch, the mass of the building is spread throughout the structure, decreasing its trust above windows and doors. According to Newton’s second and third laws of motion, when mass is exerted in one direction it will cause proportional, yet opposite force on that particular system. through the use of calculus, Gothic architecture confirmed that mass is inversely proportional the rise-to-span ratio (Sykes).

References

Branner, R. “Villard de Honnecourt, Archimedes, and Chartres.” Journal Society of Architectural History 19.3 (1960): 91-96. Document.

Huber, Michael R. “The calculus of Gothic architecture.” Journal of Mathematics & the Arts 3.3 (2009): 147–153. Document.

Sykes, M. A Sourcebook of Problems for Geometry Based upon Industrial Design and Architectural Ornament. Parsippany, NJ: Dale Seymour Publications, 1900. Hardcover.

Toman, R. Gothic: Architecture, Sculpture, Painting. New York: Tandem Verlag, 2007. Hardcover.