Why Normal Distribution Called “Normal”, Essay Example

The normal distribution curve and the term “normal” was provided by the statistician Karl. E. Pearson. It was in 1893 that the Laplace-Gaussian curve first achieved prominence. It has been criticised from the viewpoint that, in the interpretation of priority, it has led other people to believe that all the other distributions of frequency are potentially abnormal. (Gravetter, F.J. 2010)

The formulae for the curve is expressed as follows:

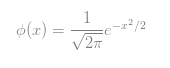
The normal curve has become one of the widest accepted and applied mathematical tools. The shape is the of a symmetrical bell shaped curve. In the defining of normal distribution both extremely large values and extremely small values are rare and often located at the tail ends of the curve. (Lyman O. 2010)

The normal distribution has also been referenced as that of the Gaussian distribution and resides within the family of probability distributions. It is widely used in quantitative expressions within the field of mathematics. The distribution is considered normal because 68 % of all the values reside within one standard deviation and within two standard deviations 95% and within three 99.8% as such in mathematical terms only 1 in 1000 values will reside outside of six sigma. As such it becomes the ideal standard by with others may be compared. (Kirk, R.E. 2007)

In the example to the right we can observe a normal distribution and the bell curve. (ITT Tech, 2013).

References

Frederick J. Gravetter, L. B. (2010). Essentials of Statistics for the Behavioral Sciences. New York: Cengage Learning.

ITT Tech. (2013, 1 20). Normal Distribution. Retrieved from ITT Tech: http://www.mathsisfun.com/data/standard-normal-distribution.html

Kirk, R. E. (2007). Statistics: An Introduction. New York: Cengage Learning.

Lyman Ott, M. L. (2010). An Introduction to Statistical Methods And Data Analysis. New York: Cengage Learning.