Electric Field and Electric Potential, Lab Report Example

Abstract

This is an electric field and electric potential lab. We conducted a comprehensive experiment that proved a valid existence of the relationship between equipotential lines and the electric field lines. It was found that the slope of the linear fit depicts that the electric field runs perpendicular to the potential lines, whose electric field is uniform.

Also the Validity of Gauss’s law was also put to the test. By measuring the E-field outside the outermost cylinder, the result was found to be consistent with Gauss’s Law.

Introduction

Objectives

In this lab we studied the electric fields between two parallel metal bars and using a water bath we mapped out the equipotential, plotted the electric fields and determined the electric field.

This helped us understand the relationship that exists between the equipotential lines and the electric field lines.

We determined the electric potential that is produced by a given set of electrodes that are held at a fixed voltage.

We will be experimenting on the validity of Gauss’s law and the principle of superstition.

Experiment

We created the experimental set-up according to the diagram that was provided in the lab guide.

Apparatus

• AC source
• Water Tank
• Electrodes
• Digital Multi-meter
• Single-Point Lead Probe
• Two-Point Lead Probe
• Conducting Ring
• Coaxial Rings (different sizes)

Procedure

Part 1

We created the experiment as had been provided in the lab guide.

We used an AC source to generate the field in the water tank as a DC source would result in the build-up of charge near the electrodes.

We used the Digital Multi-Meter to measure the RMS voltage drop between a selected fixed location and a number of various locations in the tank.

Using the single lead probe, we measured the potential of a number of equally spaced points in between the two electrodes.

We then recorded the voltage measurement from the DVM directly on a sheet of paper

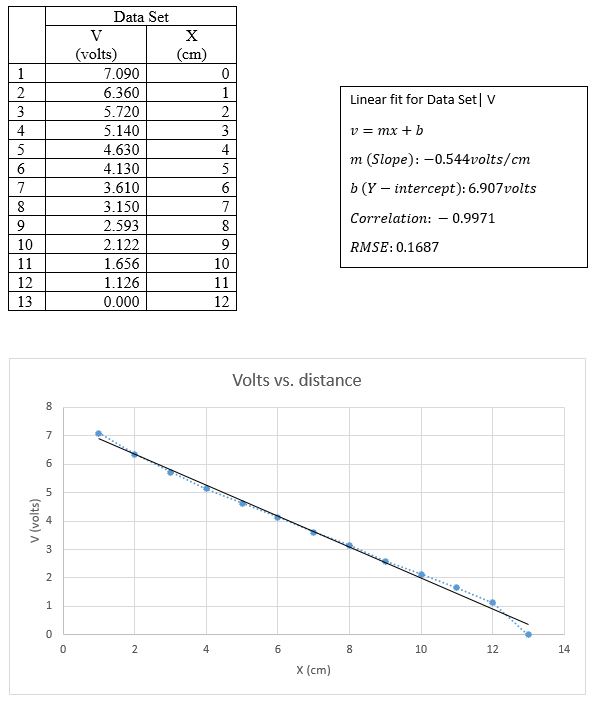
In GA, we made a graph of voltage V vs. distance x from the grounded bar.

We then added the conducting ring in the centre of the two bars and drew appropriate equipotential lines (error for this part was ignored).

We then used the signal generator to generate an AC signal between the two bars.

We picked one of the two bars as the fixed location for the black lead from the digital multimeter. This was the selected location at which the potential is zero.

We used the red digital multimeter lead to measure RMS voltage at various location within the tank.

We then switched to the two-point probe and checked the electric field outside the ring at three locations.

We rotated the probe until the DMM gave the largest possible RMS. This was to determine the direction of E.

Part 2

Turn of the signal generator and remove the bars and the ring from the tank

Set up a pair of oppositely charged coaxial rings in the water tank (i.e. the largest and the smallest rings available)

Connect the leads for the signal generator directly to the rings using the alligator clips.

Make predictions of whether the cylinders themselves will be equipotentials.

Make measurements to test prediction

Using the inner ring as location of zero potential, measure the RMS voltage at 5 different distances measured from the common axis. All the five distance are larger than the radius of the ring and smaller than the radius of the outer ring.

For each distance make measurements of the distance r, (measuring V_rms) at angles of 0°, 90°, 180°, and 270° from the positive X axis.

Compute the average value for V_rms for each distance.

Tabulate and graph these results.

Switch to the fixed spacing probe assembly and make measurements of the electric field in between the two circles.

Measure the electric field every 1.0 cm along two different direction –x and y.

Record the E values as well as the distances r from the centre of the circles, choosing the r value at a point exactly in the middle of the probe tips.

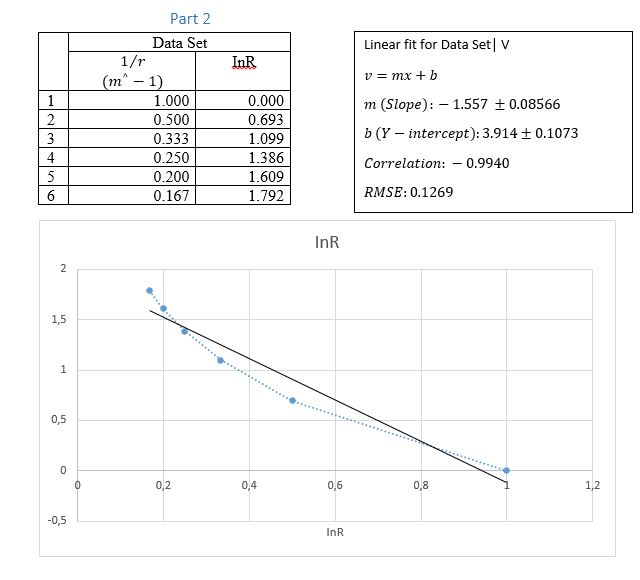
Enter the measured E values and the corresponding r values in a graph. Plot E vs. 1/r making use of the calculated column option as needed.

Use the slope of the straight-line relationship to make determination of the charge per unit length of the inner ring and its error.

We then measured the E-field outside the outermost cylinder.

Experimental Data

Part 1

Experimental Data

Part 2

Results

Part 1

The slope of the linear fit depicts that the electric field runs perpendicular to the potential lines, whose electric field is uniform.

The electric field strength inside the ring is zero.

Since work is zero, force is perpendicular to motion. Force in this case is in the same direction as E. therefore, motion or the direction of motion is perpendicular to E.

The RMS measurements inside the ring confirm that the field inside the ring runs perpendicular to the potential lines, hence the RMS recordings inside the ring have a negative value as compared to the ones outside the ring.

Part 2

After measuring the E-field outside the outermost cylinder, the result was found to be consistent with Gauss’s Law:

Using point 0.500

The fact that E is proportional to 1/r is consistent with the linear dependence of the electric potential on In(r). The electric field is directly proportional to the inverse of the distance from the centre of the wire to the field point. This is because the distance from the centre of the wire determines the strength of the electric field as the field are generated or originate from the centre of the wire. Tis same concept is applied in the electric field of the inner ring as it is described by the potential difference between the inner ring and the second point at the same distance r.

Conclusion

The experiment was a success as it proved there is a valid existence between the equipotential lines and the electric field lines. This was proven by the slope of the linear fit, which depicted that the electric field runs perpendicular to the potential lines, whose electric field is uniform. The electric field strength inside the ring was found to be zero and since work is zero, force is perpendicular to motion. Force in this case is in the same direction as E. therefore, motion or the direction of motion is perpendicular to E.

The Validity of Gauss’s law was also proven with measuring the E-field outside the outermost cylinder. The result was found to be consistent with Gauss’s Law:

Using point 0.500