Slope Stability and the Mechanics of Soils, Essay Example

Abstract

In all constructs, accurate calculations regarding the slope stability and soil mechanics is crucial to the longevity of the structure. The progression of the science of engineering has led to numerous operational models designed to make these calculations; however not all models are accurate and can provide the needed information in all situations. The multitude of surface and ground conditions existent in the real world as well as the variations of climactic circumstances can render acquiring real results a challenging if not impossible feat. This discourse will discuss the Culmann’s Method, Taylor’s Method, and simplified Bishop Method for determining the slope stability of soil and examine two real life cases of the Idukki District, in Kerala, India and the Sance Rockfill Dam in the Czech Republic, detailing the methods used for their safety, slope stability, and soil mechanics assessments. An analysis of the factorial components of soil analysis and slope stability and the results of the two case studies will follow to conclude with a summary that will seek to answer the research question of: How does the cohesive and friction angle effect the safety factor in different methods?

Slope Stability and the Mechanics of Soils

Introduction

Although the majority of major construction projects require temporary construction slopes, use of the right type of temporary excavation slope is critical and highly dependent upon the type of soil being built upon and the kind of structure being erected. Building foundations, pipe trenches, bridge piers and dams are common examples of projects that all require different standards of supportive foundations and, if it is too steep it can collapse, causing delay, extra cost and even death (Duncan & Wright, 2005). If the slope is too flat, unnecessary and expensive excavation and backfill will be required and it must also be determined if there are nearby obstructions or structures that must be protected, whether bank shoring will be required, if the ground stands on a slope steep enough to eliminate or minimize the shoring, and many other considerations vital to the success of the project and the stability of the structure (Duncan & Wright, 2005). In addition to these considerations, issues of crew safety must also be stringently accounted for when considering construction slope stability and the four types of OSHA acknowledged rocks, which are Rock, Type A, Type B and Type C, due to the different safety regulations that need to be adhered to when cutting into each type, as geotechnical reports often sidestep the issue by merely citing these guidelines or offering unrealistic solutions that must be ignored (Duncan & Wright, 2005). The lack of direct solution for conducting a thorough analysis of a construction excavation bank makes solving an accurate solution for bank stability is one of the most complex and tedious procedures in civil engineering and this examination seeks to determine how does the cohesive and friction angle effect the safety factor in different methods of slope stability analysis, like the Culmann, Taylor, and simplified Bishop methods.

Methods

Culmann’s Method

Francais-Culmann’s method of slice stability analysis primarily pertains to seismic conditions and steep slopes and uses a closed form solution to express simple equations (Ling, Mohri, & Kawabata, 1999). Much research has shown the Culmann method as a superior technique for slope stability analysis on steep slopes such as those often exhibited in loessial or windblown deposits of fine-grained, calcareous silt or clay, soils (Ling, Mohri, & Kawabata, 1999). One explanation for this is that failure slopes on vertical loessial soils can be best estimated by planes. The Culmann method uses failure planes versus failure arcs and is thus a better choice when planar failures on steep slopes are involved and is based on the Coulomb equation and planar failure model, as follows:

? = µ?_n + C_O, where ? is the shear stress at failure m is the coefficient of friction and ?_n is the normal stress on the plane at failure C_O is the cohesive strength of the material (Bunds, 2003). When combined with permanent displacement analysis, Francais–Culmann’s method is also beneficial for preliminary slope design via pseudo-static stability analysis that uses a mechanism at a prescribed failure plane, assuming the inertia force is due to an earthquake and only creates horizontal acceleration for a failure soil mass along a prescribed plane (Ling, Mohri, & Kawabata, 1999). However, recent earthquakes recorded significantly large vertical accelerations as large as that of horizontal acceleration and the effects of the vertical acceleration on the seismic performance of earth structures remain unknown (Ling, Mohri, & Kawabata, 1999).

Taylor’s Method

In 1948, Taylor established the square root of time (?) method grounded on the hypothesis that the hydrodynamic process can govern up to 90% amalgamation and encompasses identifying a straight line from the linear segment of the oedometer ? consolidation curve and utilizing it to contrive the second straight line that traverses the ? consolidation curve at 90% consolidation (Muntohar, 2007). The juncture in which the consolidation curve diverges from this uninterrupted line gives the time of 60% consolidation, enabling the coefficient of consolidation to be calculated by replacing the time of 60% consolidation into the equation

where T = c_vt

H²

and c_v = the coefficient of consolidation; H = the maximum drainage distance; t = the time elapsed from the application of pressure increments; and M = ?(2m + 1)/2 and when the values of t, T, and H are known, the coefficient of consolidation can be determined by substituting T₆₀ = 0.286 and consolidation time t₆₀ corresponding to 60% consolidation (Muntohar, 2007). However, the primary trouble with using this method is that when the consolidation curve is near 90% consolidation may be significantly affected by secondary compression the shape of the ? consolidation curve could also be affected by the secondary compression proposed simplified Taylor t method by drawing a straight line passing through the linear portion of the measured t consolidation curve (Muntohar, 2007).

Simplified Bishop Method

Like a number of algorithms, the 2D method of slices uses the system of columns as a natural extension of the traditional technique, which ignores all inter-column influences, and “…the express neglect of the vertical intercolumn shear forces leads to conservatism when kinematics of the slide require strong internal distortion” (Hungr & Byrne, 1989, p.679). Bishop’s simplified method was extended into three dimensions, which also neglects vertical inter-column shear forces, relying on the two major assumptions relative in Bishop’s theory, which are that “vertical inter-column shear forces are negligible” and “the vertical force equilibrium of each column and the overall moment equilibrium of the column assembly are sufficient conditions to determine all the unknowns” (Hungr & Byrne, 1989, p.679). The straight force symmetrical circumstances in both the longitudinal (y) and oblique (x) tendencies are neglected, just as they are in the 2D method and the total normal force acting at the base of each column is derived from the vertical force equilibrium as shown:

N = W-cA sin ?_y/ F + uA tan Ø sin ?_y/ F

m?

where W is the total weight of the column, u is the pore pressure at the center of the column base, c is the cohesion, ø is the friction angle, F is the factor of safety, and

M? = cos ?_z (1 + sin ?_y tan Ø/ F cos ?_z) (Hungr & Byrne, 1989, pp.679-680). The factor of safety is derived iteratively from the sum of moments around a common horizontal axis, parallel with the x-axis:

F = ? [cAR + (N – uA)R tan Ø]

 ? Wx – ? Nf cos ?z/ cos ?y + ? kWe + Ed (Hungr & Byrne, 1989, p.680)

In this equation, R, x, and f are the moment arms of the resisting force, column weight, and normal force correspondingly, and, when dealing with a horizontal earthquake force, equivalent to an acceleration of k times g is expected to function at the center of each column, with a moment arm of e (Hungr & Byrne, 1989). Additionally, ? is the result of all parallel mechanisms of applied point loads, with a moment arm d (Hungr & Byrne, 1989). In regards to the rotational surface, the reference axis is also the axis of rotation and f is zero in each support, but the result will depend on the position of the reference axis in the case of a non-rotational surface (Hungr & Byrne, 1989)

Background of Cases

Slope Stability Analysis: Idukki District, Kerala

In the Idukki district of Kerala, India, there are frequent incidences of slope failures, especially beside the road cuttings and hill slopes, and such events cause traffic jams, property losses, and deaths (Sreekumar, 2009). Such losses necessitate a judicious assessment regarding the stability of slopes along the hill roads and this case study seeks to analyze the stability of “…a typical hard rock profile at Chuzhappu and a lateritic profile at Kumili along the road connecting Kottayam and Kumili” (Sreekumar, 2009, p.813). An examination of the various influences has been conducted and analyzed, determining that the positioning of discontinuities is one of the most important characteristic affecting slope instability along the hard rock profile of Chuzhappu (Sreekumar, 2009). These areas have been analyzed carefully using various means to ascertain the severity of the rock slides that can happen in these circumstances and to ascertain the potential susceptibility to slope failure due to the e power of the water contacting the discontinuities during heavy rain fall, which further the down slope movement (Sreekumar, 2009). The homogenous nature of the laterite slope at Kumili enabled researchers to adapt the Bishops and Swedish methods for stability analysis (Sreekumar, 2009).

The study also investigates the effectiveness and applicability of the techniques implemented in soil mechanics to determine the solidity of this laterite slope in comparison to results garnered in actual field conditions, which indicates that two zones at Chuzhappu and one subdivision at Kumili are at the geological verge of malfunction, especially when piezometric head rises during a rainstorm (Sreekumar, 2009). It is also suggested that these procedures are highly useful in determining the Factor of Safety (FOS) in synopses with comparable terrestrial locales since slope failures in Kumili may be caused by the collective influence of ground water and the relative weak unified attributes of lateritic rocks (Sreekumar, 2009). However, under ordinary dry conditions when all areas have superior FOS rates, which consequently, leads to an increase in pore pressure, and during rainstorms, the shearing resistance diminishes and the likelihood of breakdown is heightened (Sreekumar, 2009).

Safety Assessment: Sance Rockfill Dam

The 62 meter high Sance Rockfill Dam constructed in the late 1960s created a drinking water reservoir that is now a key source of water supply of the Moravian- Silesian region in the Czech Republic (Dolezalova, & Hladik, 2011). The observational outcomes gathered over more than 30 years have revealed considerable deposits and horizontal movements of the summit, which, combined with the sheer downstream slope, jeopardized the security of the dam (Dolezalova, & Hladik, 2011). In addition, the substandard spillway dimensions necessitating rebuilding of the spillway, upgrading the maximum water volume up to the top and amplifying the breakwater on the pinnacle of the dam (Dolezalova, & Hladik, 2011). Regulated 2D and 3D models appropriated for the monitoring results applied for the safety assessment of the dam, including slope stability exploration as well as valuation of the clay core cracking and hydraulic fracturing hazard (Dolezalova, & Hladik, 2011). The detection of the unfavorable deformational trends displaying a constant creep rate have caused structural changes of rockfill due to grain breakage and collapse settlement due to wetting (Dolezalova, & Hladik, 2011). Overall, the observed results supported the rehabilitation model for the dam and further performance projections extending up to 2050 were predicted based on the solutions implemented for the coupled mechanical-hydraulic-viscoplastic problems with an account for unsaturated flow in the clay core (Dolezalova & Hladik, 2011).

Analysis

Introduction

The basis of the rockfill dams design is dedicated to safeguarding the strength of the structural configuration under several predetermined conditions, as can be expected to occur with contained earth during the life of the dam. The collective mechanical and hydraulic conditions must be taken into consideration since pore pressures develop during construction, after impoundment and in drawdown (Alonso & Cardoso, 2010). Considerations also include instability trends caused by transient flow and internal erosion, which will affect the fundamental expectations regarding the hydro-mechanical behavior of customary and non-traditional materials used in the construction of dams (Alonso & Cardoso, 2010). The materials used for dam construction are compacted unsaturated materials ranging from clayey to rockfill and the current understanding on the behavior of modern materials used in the construction of dams is the basics of the study of soil mechanics (Alonso & Cardoso, 2010; Duncan & Wright, 2005). This analysis will detail the mechanics of soil in regards to slope stability, downward slope force, the effects of groundwater and seepage, as well as numerous other attributes of the landscape to determine the effects of the cohesive and friction angle in regards to the safety factor when using different methods.

Soil Mechanics

The field of slope stability involves the examination of the resistance of an inclined surface to failure of sliding or collapsing and includes the analysis of static and dynamic stability of slopes of earth and rock-fill dams, as well as other types of excavated slopes, embankments, levees, and natural slopes in soil and soft rock (Duncan & Wright, 2005). Slope stability investigation includes modeling, analysis, and design mitigation is usually completed by engineering geologists, geologists, or geotechnical engineers (Duncan & Wright, 2005). The two factors that have the greatest effect on slope stability are slope gradient and groundwater. The overall consensus is that the greater the slope gradient and the more groundwater present, the less stable said slope will be, regardless of the geologic consistency or soil type (see Figure 1), which makes it essential for engineers to understand why slope gradient and groundwater are so important to slope stability if they wish to successfully locate, design, construct, and maintain roads (Duncan & Wright, 2005).

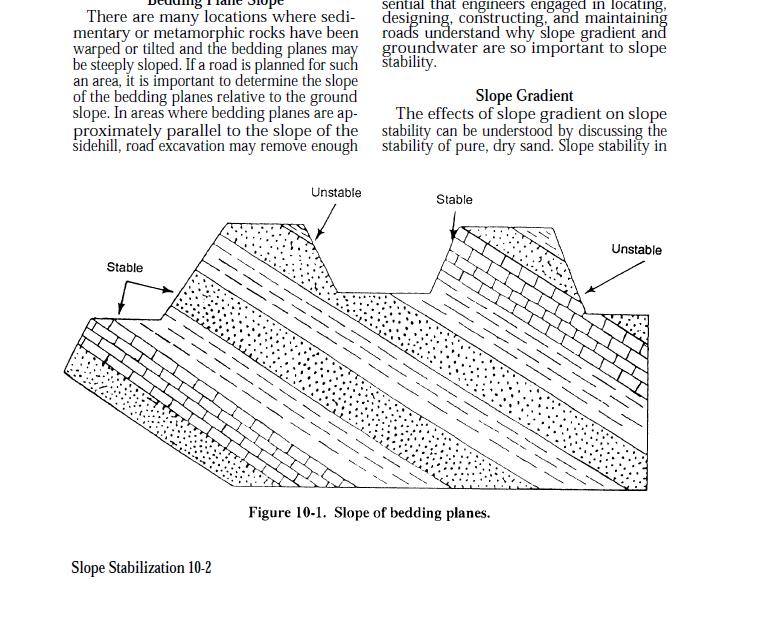
(Duncan & Wright, 2005)

Slope Gradient

The slope gradient is basically the incline of the slope and directly affects the stability of the slope as well as the cohesiveness and frictional qualities, which are both relative to the bearing capacity (Duncan & Wright, 2005). This factor and its relevance can best be understood when regarded from the perspective of the frictional stability and sliding resistance of pure, dry sand (Duncan & Wright, 2005). Slope stability in sand is contingent entirely on frictional resistance to sliding, which is based on the slope gradient affecting the portion of the weight of an object that rests on the surface and the coefficient of friction (Duncan & Wright, 2005). When considering normal force, the segment of the mass of an object that rests on a surface is the normal force (N) because it lies perpendicular or normal to, the surface and N changes as the slope of the surface changes. When the incline of a surface changes the normal force of an object resting on the surface is affected by this slope gradient differential, with the affect being directly proportional to the weight of the object and the surface incline. In the case of a vertical surface, there is no weight on the exterior, so the standard force is zero. The coefficient of friction changes the typical intensity of frictional resistance to sliding (F) with slope gradient (Duncan & Wright, 2005)

Downslope Force.

The downslope force is the component of the gravitational influence acting in the downslope direction proportionate to the weight of the object and its ability to generate resistance to the frictional resistance to sliding (Duncan & Wright, 2005). This is also known as the driving force and is directly dependent upon the slope gradient and increases as the gradient increases until the gradient becomes steep enough to surpass the frictional resistance to sliding and the block slides (Duncan & Wright, 2005). If the slope gradient is less than 70%, the frictional resistance to slide will be greater than the downslope of the object, so it will remain stable on the surface, but if the slope gradient is greater than 70%, the object will slide because the driving force will surpass the frictional opposition to sliding (Duncan & Wright, 2005). Although principally tested in pure, dry sand, which is seldom found in soils, the theories of the effects of frictional resistance and slope gradients can be applied to any dry topsoil (Duncan & Wright, 2005).

Shear strength is a soils’ ability to resist sliding along internal surfaces within the soil mass and the structural strength of a foundation is primarily a function of shear strength (Alonso & Cardoso, 2010). Shearing occurs when a block of packed soil fails, or slides with one section of the block moving past another portion in a parallel direction (Duncan & Wright, 2005). The surface along which this shearing action takes place is called the shear plane, or the plane of failure and shear strength is measured by the ability of the soil to resist movement between particles because of physical bonds from particle interlocking, atoms sharing electrons at surface contact points, and the formation of chemical bonds or cementation reactions, like crystallized calcium carbonate (Duncan & Wright, 2005). Such resistance to shearing is often referred to as shear strength and pure sand cultivates shear strength through frictional resistance to sliding, but pure clay acquires shear strength because the separate particles develop cohesion (Duncan & Wright, 2005). Collectively, the shearing strength is influenced by the soil composition, including the mineralogy, grain size and distribution, pore fluid type and content, shape of particles, and the ions on the particles and in pore fluid; the initial state of the soil, as in the looseness, density, consolidation, and other attributes; and the soil structure, which denotes the constitution of elements within the soil mass, the way in which the fragments are saturated or disseminated (Nicklin, Remus, & Conroy, n.d.).

The presence of features such as layers, voids, pockets, cementation, and other parts of the structure of clay affect the shear strength of the soil over that of pure sand because of the cohesive nature of the clay. Dry clay has substantial shear strength, but as dry clay absorbs water, its shear strength is diminished because the water separates the clay particles and reduces the cohesive bonds (Nicklin, Remus, & Conroy, n.d.). The structure of the soil controls how much water will absorbed and, subsequently, to what degree the shear strength will decrease upon saturation (Nicklin, Remus, & Conroy, n.d.). However, there are some types of topsoil, such as illite and kaolinite, that maintain their integrity even when saturated, although montmorillonite displays a significant decrease in slope stability when saturated and “…saturated illite and kaolinite clays have about 44 percent of their total volume occupied by water compared to about 97 percent for a saturated montmorillonite clay “(Nicklin, Remus, & Conroy, n.d., p.3). This accounts for why montmorillonite clay has such a large change in volume between its wet and dry states, which is known as a high shrink-swell capacity, and saturated muds of this type have low shear strengths, which is why these types of soil have a significant effect on slope stability (Nicklin, Remus, & Conroy, n.d.). Overall, the proportional solidity of soils is contingent upon a combination of “…their shear strength and the downslope component of the weight of the soil” and soils consisting of “…the same geologic material, the soil with the higher percentage of illite or kaolinite clay has greater shear strength than a soil with a significant amount of montmorillonite clay” (Nicklin, Remus, & Conroy, n.d., p.3).

Groundwater

Groundwater is made up of the waters derived from rainfall that are held underground in the soil or in pores and crevices of rocks (Xu, Li, & Chen, 2007). It is common for hill slopes, side slopes, or drainage ways to be completely secure during the summer and for slides to occur following the winter rains begin, which can primarily be attributed to the shift in the volume of water in the pores of the soil (Xu, Li, & Chen, 2007). It is easiest to understand the effect of groundwater on slope stability by again examining these relational aspects using sand and considering that the frictional resistance to sliding in dry sand is developed as the product of F and N acting on the surface of the failure plane (Gedeon, 1992). Closer scrutiny of this circumstance demonstrates that each grain of sand is interconnected, or jammed together, by the overall force of the mass of sand and the greater the magnitude of the force causing this meshing of sand grains, “…the greater is the ability to resist the shear force that is caused by the downslope component of the soil weight” (Nicklin, Remus, & Conroy, n.d., p.3). However, the increase in groundwater causes buoyant forces to be exerted on each grain of sand as it becomes submerged, which reduces the normal force because of the buoyant force (Xu, Li, & Chen, 2007).

Seepage Force

Groundwater also contributes to slope instability in another way, which is through the seepage force of groundwater as it moves downslope (Duncan & Wright, 2005). As detailed in Gedeon (1992), “…the seepage force is the drag force that moving water exerts on each individual soil particle in its path” which promotes to the dynamic power that drives masses of soil downslope (p.2-8). This concept is easily illustrated by the effortlessness in which “…coarse-textured soil may be dislodged from a road cut bank when the soil is conducting a relatively high volume of groundwater” (Gedeon, 1992, p.2-8).

Rock falls and Rockslides

Rock falls and rockslides typically occur in areas with imbedded sedimentary deposits, like gigantic sandstone, and the beds are undercut by stream erosion or road excavation (Xu, Li, & Chen, 2007). Stability is sustained by the placement of the rock, which establishes frictional resistance within the bedding planes, and these elements are mainly significant where the bedding planes plunge downslope toward a road or stream (Xu, Li, & Chen, 2007). Sudden occurrences, such as rockslides, happen with great speed and can extend a great distance, consisting of fractured rock debris and exceptionally large boulders (Gedeon, 1992). The danger to human and livestock safety mandates that roadways prone to potential rockslides or rock falls be inspected by professionals that can assess the integrity of the rock and gauge the dip of the bedding planes (Nicklin, Remus, & Conroy, n.d.).

Debris Avalanches and Debris Flows

Debris avalanches and debris flows are two closely related types of slope failure that generally occur on superficial, gravelly soils that are comparatively low in clay material on slopes over 65 percent and are especially frequent on slopes over 75 percent (Duncan & Wright, 2005). Debris avalanches consist of a rapid downslope flow of a multitude of rocks, loose soil, and forest debris holding capricious amounts of water, similar to shallow landslides that ensue from frictional letdown adjacent to a slide exterior that is fundamentally parallel to the topographic surfaces that are created where the accrued tensions surpass the resistance to shear (see Figure 2) (Duncan & Wright, 2005).

Figure 2: Debris Avalanche

(Duncan & Wright, 2005)

As it detaches from the mound, the soil layer slides downslope above an impervious periphery within the debris or at the unseasoned bedrock surface and constructs a disordered deposit at the base and the substantial increases in water content causes the debris flow to become an avalanche downslope (Duncan & Wright, 2005). Often, the sudden influx of water decreases the shear strength of earth material on a steep slope, and they typically follow heavy rainfall (Duncan & Wright, 2005).

Stable Slope Construction in Bedded Sediments

The construction of secure thoroughfares requires more than a basic grasp of regional geology and soil mechanics but also precise, comprehensive statistics on the physiognomies of the soils, groundwater, and geology where the road will be built (Gedeon, 1992). It is necessary to develop methods that will help determine soil and vegetative indicators of slope instability, techniques on road location and high groundwater level indicators (Duncan & Wright, 2005). Since bedded sediments vary from soft siltstone to hard, massive sandstone, these geologic substances combine with the geologic progressions and the effect of climate changes over long periods of time to influence slope gradient, soil quality, and the speed of erosion (Gedeon, 1992). These dynamics also influence the specific type of slope stability problems that are likely to be encountered and are most commonly associated with distinctive sites within the bedded sediments, which are sandstone, Types I and Type II, deeply weathered siltstone, and sandstone adjoining ridges of igneous rock (Duncan & Wright, 2005).

Results

The slope stability analysis of the Idukki District in Kerala, India revealed that the noted functioning of the dam is due to physical changes of rockfill caused by the characteristics of the sandstone and the amount of compaction of the fill, which do not correspond with a dam of this height. Although there was no transversal cracking vulnerability to the clay core projected and the longitudinal stability hazard was limited to a hypothetic loading cases based on rapid rises in water levels and collapse settlement of the unsaturated rockfill due to wetting, no hydraulic fracturing vulnerability to the clay core detected during the study, “…but according to the model, hydraulic fracturing in the upper part of the clay core could occur in the future (2050)” (Dolezalova & Hladik, 2011, p.85). As detailed in the study by Dolezalova & Hladik (2011),

“…in such a case the downstream filter with specific grain size distribution is designed to protect the clay core against piping. As a part of the rehabilitation of the dam, extensometers in the clay core along the crest will be installed and the longitudinal displacements of the dam carefully monitored. In order to improve the stability conditions of the downstream slope, a supporting bench will be placed on the downstream side of the dam” (Dolezalova & Hladik, 2011, p.85).

In contrast, the safety assessment of the Sance Rockfill Dam revealed that the likelihood for the incidence of collapsing exists at sector A and a wedge failure is likely to occur in sectors B and C (Sreekumar, 2009). These Sectors are stable during dry condition but the FOS becomes less than one during monsoon period. Total amount of slide debris that may be wasted on to the state highway is estimated at 1769.97 tons. The impact of this slide debris may be adequate to initiate severe slides along this highway slope causing much damage to transport and communication. Slope failures in Kumili profile may occur by the combined effect of ground water and the relative weak cohesive property of lateritic rocks. Under normal dry conditions, all the sectors have greater Failure of Safety (FOS) values. However, as a consequence of the rise in piezometric head and increase in pore pressure, during rainstorms, the shearing resistance decreases and the probability of failure is enhanced (Sreekumar, 2009).

The bearing capacity is the ability of soil to safely carry the pressure placed on the soil from any engineered structure without undergoing a shear failure with accompanying large settlements. The ultimate bearing capacity is the generally accepted method of bearing capacity analysis is to assume that the soil below the foundation along a critical plane of failure (slip path) is on the verge of failure and to calculate the bearing pressure applied by the foundation required to cause this failure condition. This is the ultimate bearing capacity qu and the general equation is:

Where:

q_u = ultimate bearing capacity pressure, kips per square foot (ksf)

Q_u = ultimate bearing capacity force, kips

c = soil cohesion (or undrained shear strength C_u), ksf

B = foundation width, ft

W = foundation lateral length, ft

= effective unit weight beneath foundation base within failure zone, kips/ft3

= effective soil or surcharge pressure at the foundation depth D, D, ksf

= effective unit weight of surcharge soil within depth D, kips/ft3

= dimensionless bearing capacity factors for cohesion c, soil weight in the failure wedge, and surcharge q terms

= dimensionless correction factors for cohesion, soil weight in the failure wedge, and surcharge q terms accounting for foundation geometry and soil type” (Gedeon, 1992, pp.1-2,1-3).

Conclusion

The slope stability and mechanics of soils re the determining elements regarding how the cohesive and friction angle effects the safety factors in different methods. When the bearing pressures exceed the limits of the shear resistance of the soil, this causes failure of the edifice which is usually accompanied by tilting (Gedeon, 1992). A bearing capacity failure can result in large downward movements of the structure, and usually occurs within one day following the application of the first full load to the soil (Gedeon, 1992). Even without full failure occurring, “…excessive settlement and differential movement can cause distortion and cracking in structures, loss of freeboard and water retaining capacity of embankments and dams, misalignment of operating equipment, discomfort to occupants, and eventually structural failure” (Gedeon, 1992, p.1-10). Proper settlement analyses must be performed frequently to establish the expected foundation settlement and cohesive and friction analyses must also be performed to ensure that these elements will not be contribute to the failure of the dams. Both total and differential settlement between critical parts of the structure must be compared with allowable values and a true “…calculation of the bearing pressure required for ultimate shear failure is useful where sufficient data are not available to perform a settlement analysis” (Gedeon, 1992, p.1-11). Suitable safety precautions must ne implemented to ensure that the probability analyses predicting failure in the designated areas are accounted for and prevented. Furthermore, structures like silos, embankments and uniformly loaded tanks, and mats established on soft soils and intended to endure large settlements all may be vulnerable to a base shear failure (Gedeon, 1992).

References

Alonso, E., & Cardoso, R. (2010). Behavior of materials for earth and rockfill dams: Perspective from unsaturated soil mechanics. Frontiers of Architecture and Civil Engineering in China, 4(1), 1-39. Retrieved from ABI/INFORM Global. (1964630881).

Bunds, M. (2003, February 14). The Coulomb – Navier Failure Criterion and Byerlee’s Law. Dept. of Earth Science, Utah Valley State College. Retrieved from http://research.uvu.edu/Bunds/GEOL3700/Handouts/cn_byerlees_law_mohr_circle.pdf

Dolezalova, M., & Hladik, I. (2011). Long-term behavior and safety assessment of Sance Rockfill Dam. Frontiers of Architecture and Civil Engineering in China, 5(1), 79-89. Retrieved from ABI/INFORM Global. (2251762991).

Duncan, J.M. & Wright, S.G. (2005, January). Soil strength and slope stability. Texas: John Wiley & Sons. Inc.

Gedeon, G. (1992, October 30). Bearing capacity of soils. Department of the Army, U.S. Army Corps of Engineers CECW-EG Washington, DC, EM 1110-1-1905

20314-1000. Retrieved from http://www.cedengineering.com/upload/Bearing%20Capacity%20of%20Soils.pdf

Ling, H.I., Mohri, Y. & Kawabata, T. (1999). Seismic analysis of sliding wedge: extended Francais–Culmann’s analysis. Soil Dynamics and Earthquake Engineering, 18, 387–393.

Nicklin, M.E., Remus, J.I., & Conroy, J. (n.d.). Gully Bank erosion of loesslal soil in urbanizing watersheds. University of Nebraska-Lincoln, Lincoln, Nebraska; U.S. Army Corps of Engineers, Omaha, Nebraska; U.S. Navy Corps of Engineers. Retrieved from http://iahs.info/redbooks/a159/iahs_159_0141.pdf

Sreekumar, S. (2009). Techniques for slope stability analysis: Site specific studies from Idukki district, Kerala. Journal of the Geological Society of India, 73(6), 813-820. Retrieved from ProQuest Science Journals. (1892269731). http://fast10.vsb.cz/lahuta/Liter/Mesoil/obfound.pdf

Xu, Q., Li, X., & Chen, Z. (2007). Three-dimensional stability analysis of the dam foundation at Baise. Frontiers of Architecture and Civil Engineering in China, 1(2), 217-221. Retrieved from ABI/INFORM Global. (1938861311).