Volume Error Propogation, Lab Report Example

Introduction

Objective

The objective is to find the volume and calculate the uncertainty of each dimension of the cylinder, bullet, cup and the 6 balls and understand how the uncertainty of each dimension of the volume propagates the error of the volume of the bullet.

Experiment

Apparatus

• A bullet
• A cylinder
• A cup
• 6 balls
• Vernier Callipers
• Graphical analysis

Procedure

We took several measurements of the dimensions of the cylinders, 5 time using the Vernier calliper and recorded them.

We then took several measurements of the dimensions of the bullet and recorded them

We took several measurements of the dimensions of the cup and recorded them

We finally took several measurements of the dimensions of the 6 balls and recorded them.

We took the readings and input them into graphical analysis for each of the given objects

We calculated the mean and standard deviation of the readings using graphical analysis

We calculated the volume and uncertainty of the volume.

Experimental Data

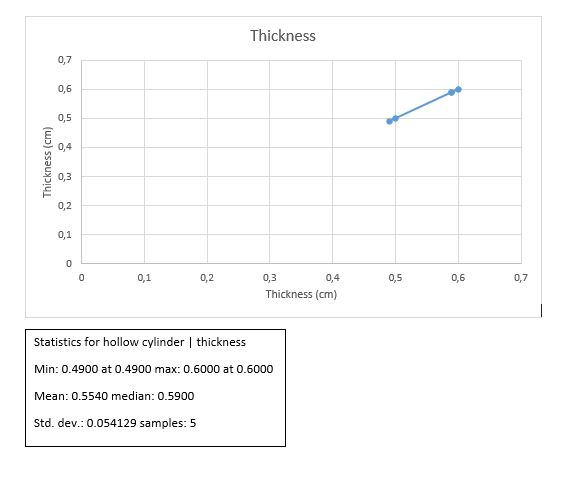
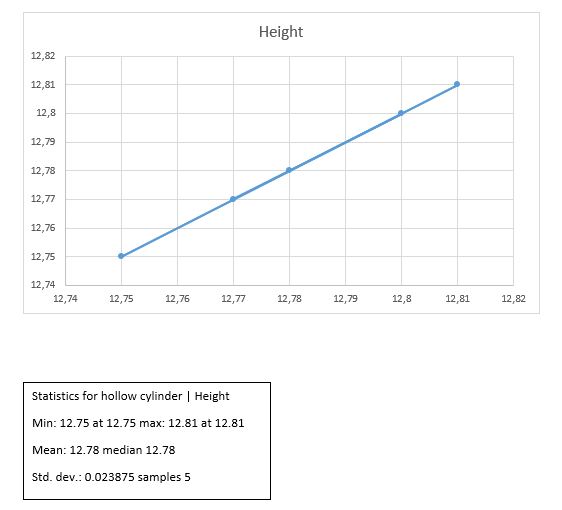
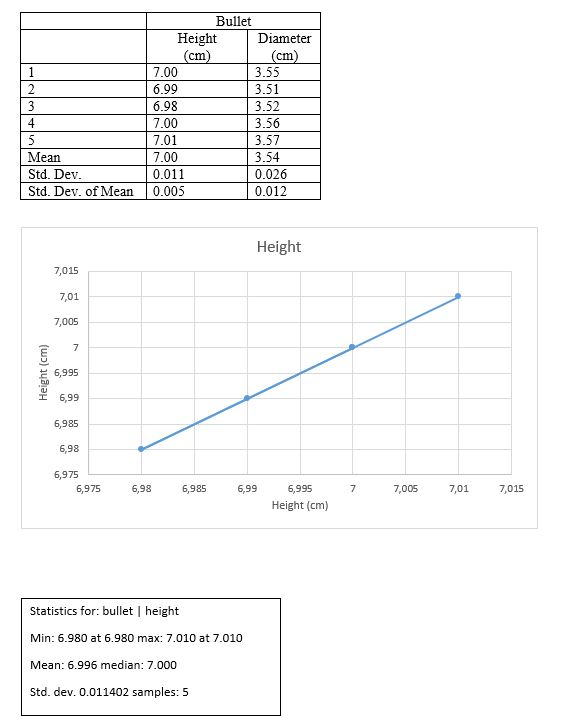
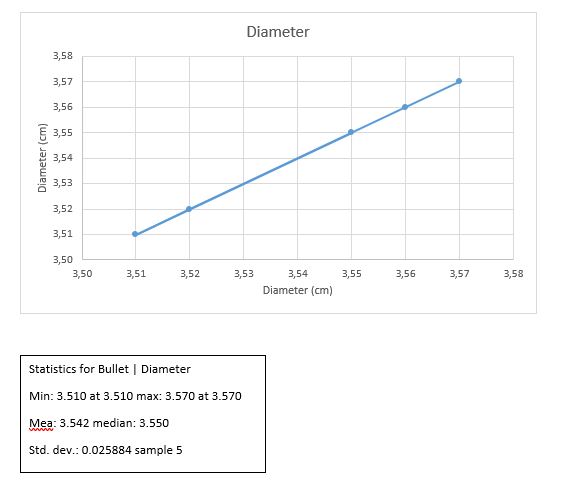
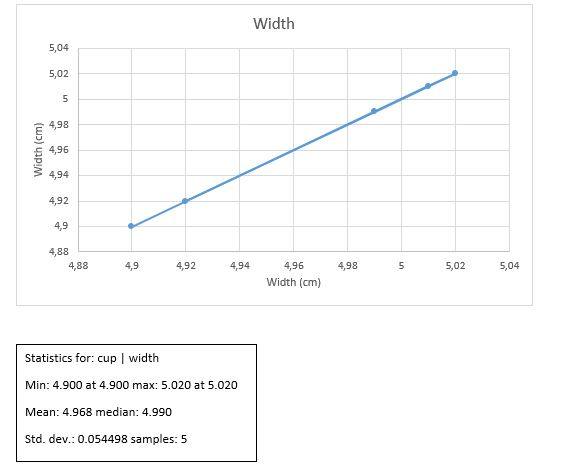
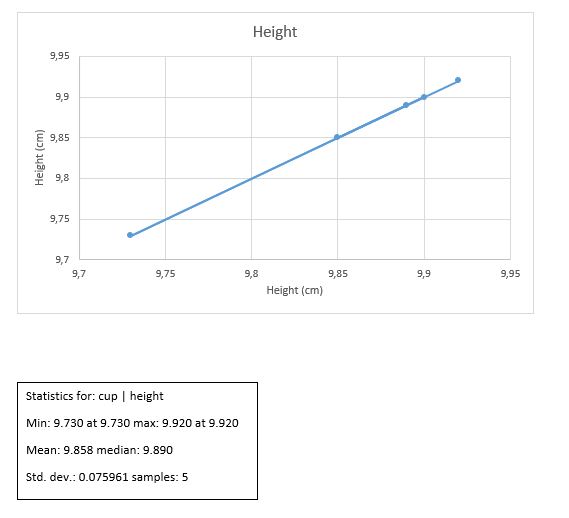
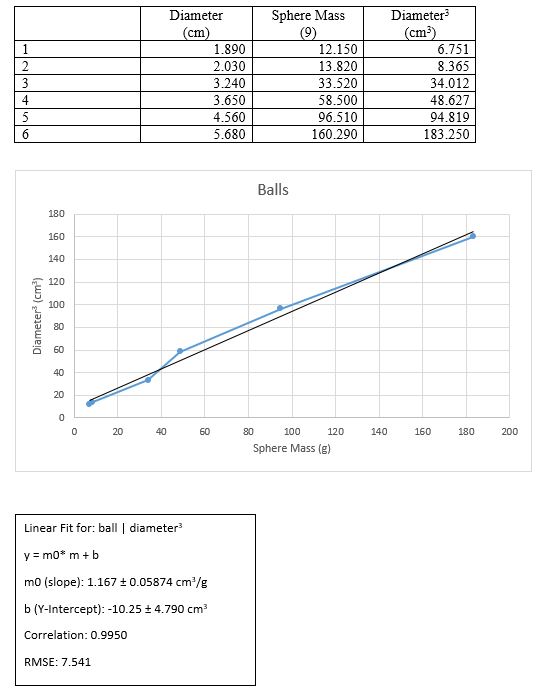
Results

Calculate the volume of the cup

H +/- ?H = 9.86 +/- 0.034 cm

L +/- ?L = 4.95 +/- 0.019 cm

W +/- ?W = 4.97 +/- 0.024 cm

V = H* L * W = 242.57 cm³

?V = [(?H * L * W)²+(2H * 2W *?L)² + (H * 2L * ?W)²]^1/2 = 4.48 cm³

V+/-?V=242.57 +/- 4.48cm³

Calculate the volume for the bullet

D +/- ?D = 3.54 +/- 0.026

H +/- ?H = 7.00 +/- 0.011

V = V_cylinder + V_hemisphere = ¼ ?D² (H-D/2) + 1/12 ?D³= ¼ (?D²H) – 1/24 (?D³)

= ¼ (? · 3.54² ·7.00) – 1/24 (? · 3.54³)

= 68.90 – 5.81

= 63.09 cm³

?V = [(¼ · ? · D² · ?H)² + {(½ · ? · D · H – 1/8 · ? · D²) · ?D}² ]^1/2

= 0.94

V +/- ?V = 63.09 +/- 0.94 cm³

Hollow cylinder

H +/- ?H = 12.78 +/- 0.011cm

D +/- ?D = 8.55 +/- 0.025cm

T +/- ?T = 0.55 +/- 0.024cm

V=1/4 · ? (D²-T²)h = 730.72cm³

?V = ((1/4 · ? (D²-T²) ?h)² + (0.5 · ? ·D · H · ?D)² + (0.5 · ? · T · h · ?T)²)^1/2

= 4.35 cm³

V +/- ?V = 730.72 +/- 4.35 cm³

Discussion

In this lab, the dimension of the bullet, cup, cylinder and the 6 balls were taken 5 times. The measurements of each of the dimensions of the objects were similar, although they did have a slight standard deviation. A suitable equation was configured for the calculation of the volume of the objects. A partial derivative was employed to help figure out the uncertainty of the volume

The actual value of the volume of the objects was found after plugging in the mean value and the standard deviation of the mean value of the volume of the bullet. The volume of the hollow cylinder can be derived from the subtraction of the volume of the inner cylinder from the volume of the outer cylinder. The volume of the whole bullet shape is found by adding the volume of the semi-sphere to the volume of the hollow cylinder. The results of the calculations make perfect sense.

Even though the value of the result of the experiment was not far off from the expected, the uncertainties associated with the bullet are high. The uncertainty associated with the height of the bullet was the highest and caused the large value in the overall uncertainty in the volume of the bullet. The most possible error in the experiment is due to our measurement of each dimension. The results of the experiment could be improved by conducting measurements more than five times. This leaves little room for error, reducing the uncertainty associated with the measurement of each dimension.

Conclusion

The volume and the uncertainty of volume was critically and carefully analysed. The error of the volume of the bullet is propagated by applying the partial derivative method. As the discussion above, the result of the volume and the uncertainty of the volume is reasonable. The possible errors are adequately covered in the discussion above.

In conclusion, the experiment met the objective of the volume lab.